幸せに楽しく生きるためにはどういう考え方やスキルが必要なのだろうかという疑問を持ち、今まで沢山の人のお話を聞いたり、楽しく生きている人の思考法を研究してきました。
そこでわかったことが、学校の勉強って実は社会でとても役立つ、最近そう感じることがとてもたくさんあります。
幸せに生きるためには、「無駄なところで損をしない」ということが大事だと私は考えています。
騙されないようにすることはもちろんですが、「最小限の労力で最大の結果を得る」ことを意識することで、お金や時間、気力などを無駄に使うことがなくなり、より自分がやりたいことに力やリソースを割くことができるようになるからです。
いろいろな人と接していく中で
あーーーー、もったいないなー!!!
と思う場面を振り返ると「数学的な考え方」ができていないことで損をする場面がたくさんあることに気づきました。
「数学」と言っても、中学校の数学の基礎の「考え方」を活用するだけなので、数学が苦手だった人でもこの記事を読めば日常で知らず識らずに損をしてしまうことがなくなります!
サクッと読める目次
私は理系じゃないから・・・という誤解
こういう話をするときによく聞くのがこの言葉。
「私は理系じゃないから、数学って言われてもわかりません・・・」
「数字は苦手だから、考えたくない・・・」
その気持ち、とってもわかります。
受験勉強では「計算を行って正しい答えをだす」ことが求められており、それはとても難しいものですし、たくさんの公式を覚えないといけません。
数学的な考え方が重要!と書いている私も正直いま受験数学の問題を目の前にしたら手が止まってしまうと思います。
受験数学はこんなイメージですよね。
○○さんが分速80mで200m離れたところから移動しています。そして、△△さんは分速60mでここから向かっていきます。すれ違うのはいつでしょうか?
ええっ、どうやるんだっけ?計算面倒だな、難しそうだな。そう思うのではないでしょうか。
でも、生活の中で必要なことは正確な秒数を算出することではありませんよね。
・○○さんと△△さんは出会うことができるのか
・それはいつ頃なのか?(1分なのか、10分なのか、1時間後なのか、というざっくり感)
こういうことがわかれば十分なのです。
この例に上げた問題であれば「分速」が1分間で進む距離であるとわかっていれば、だいたい2~3分で出会うんじゃないかなーと想像がつきますよね。
受験では1秒でも間違えたらバツになってしまうのですが、別にそれが1分早かったり、遅かったりしてもそこまで大きな問題にはならないはずです。
大事なのは「必要最低限な考え方」だけです。
難しい話をするつもりは一切ありません。
気負わずに、読み進めてもらえると嬉しいです。
日常で役立つ数学的な考え方4つのポイント
スーパーでお肉の値段を比べるのは?
まずは「単価」と言う考え方です。
こちらは普段の生活の中でも意識をされている方が多く、いまさら説明することもないかもしれません。
スーパーによく買い物に行く方であれば、毎日の買い物の中で無意識に計算している方もいると思いますので、「知ってるよ!」という方は流し読みして次に進んでもらえればと思います。
同じ価値のものであれば、少しでも安いほうがいいですよね?
ガソリンスタンドが2つあった時、
- ガソリンスタンドA:1リットル140円
- ガソリンスタンドB:1リットル135円
という料金があった場合は、ガソリンスタンドBに行きますよね?
(もちろんポイントの割引などは同じの前提ですよ!)
実はガソリンの値段はとても比べやすいようにできているのです。
それはなぜかと言うと、どこのガソリンスタンドても「1リットルあたりの値段」を表示してくれているからです。
もし、これが以下のように書いてあったらどうでしょうか?
- ガソリンスタンドA:1リットル140円
- ガソリンスタンドB:1.2リットル162円
どっちが安いのか、一瞬わからなくなりますよね?
実はどちらも最初の例と値段は変わっていないのですが、1リットルと1.2リットル、のように量が違うから比較しにくくなっているのです。
ある一定の量や大きさ(単位、といいます)あたりの値段を「単価」といいます。
ガソリンであれば1リットルあたりの値段で表すのが日本では標準ですね。
スーパーマーケットに行くと、この「量」や「大きさ」がバラバラなものが並んでいます。
例えば、以下のような例です。
私が毎朝食べているケロッグのオールブラン(シリアル)
- 250グラム○○円
- 400グラム△△円
よくセールになる鶏肉
- 1パック(238グラム)○○円
- 1パック(284グラム)△△円
野菜ジュースに入れたいにんじん
- 大きい人参3本入り○○円
- 小さい人参5本入り△△円
このように、単位が揃っていないことで直感的に比較しにくいものがたくさん並んでいます。
- ケロッグのオールブラン→100gあたりの値段で考える
- 鶏肉→100gあたりの値段で考える
- 人参→1本あたりの値段で考える、または100gあたりの値段で考える
のように、計算する癖をつけることで、高い買い物をしてしまう事がなくなります。
ということで、1つ目のポイント。
POINT1:大きさが違うものを比較するときは、単価(ある量・大きさあたりの値段)を考えよう!
ちなみに、普通は同じ商品であれば大きいほうが単価が安いのが当たり前です(ですよね?)が、
タイでは1個12バーツ!8個入り100バーツ!のように多いほうが高いという謎のトラップもあるそうです。笑
車や結婚式でどんどんオプションが乗っかる?
車を買ったり、結婚式を挙げたり、「自分の給料の数カ月分」という高額な買い物をしたことがある方は思い出してみてください。
もしそのような経験がない場合は、想像しながら読み進めてもらえればと思います。
車や結婚式は色々なオプションをたくさん提案されることになります。
車でいうと、こんな感じのオプションがあると思います。
わかりやすいように車用語を使わずに書いていきます。
- カーナビのグレードアップ:5万円
- 限定カラー:5万円
- かっこいいホイール(タイヤ):10万円
- より明るいライト:5万円
結婚式であれば、こんなオプションがあるでしょう。
- 花束のグレードアップ:3万円
- 花火:2万円
- シャンパンタワー:3万円
車も、結婚式も、もともとの値段が200万円等と高額なことがあり、それに比べてしまうと一つ一つのオプションはそこまで高くないように感じてしまいます。
「給料の数カ月分」の買い物は「一生に数回の大きな買い物」であることもとても多く「絶対に後悔したくない」という気持ちも入ってきます。
430万円の車を買おう!と決めたときに、先程の4つのオプションを提案されたとします。
確かに、カーナビは高性能な方が良さそうです。限定カラーは色に深みがあってかっこよさそうです。
ホイールやライトも、そりゃかっこいいほうがいいよなぁ、と営業マンの聞きながら考えます。
全部のオプションを付けると、430万円に5万円+5万円+10万円+5万円が追加されて、455万円になります。
430万円の普通の車と、455万円のちょっとカスタムされた車。
そう考えると、値段の差もそこまで大きくないし、営業もいい方だし、オプションをつけちゃおうかなー・・・
そう思うかもしれません。
これが、例えば100万円の車を買おうとしている、とするとどうでしょうか?
オプション無しの車と、ありの車の値段は100万円と、125万円。
少し違うように感じますよね。
もし、50万円の車だったら?
オプション無しの車と、ありの車の値段は50万円と、75万円。
結構違うように感じませんか?
ここに、落とし穴があります。
100万円単位の買い物をするときに、1万円の大小がどうでも良くなる人は結構多いような印象です。
でも、4万円のものが3万円になったら、それはそれは嬉しいですよね?
もっと言えば、急に1万円もらえることになったら、とても嬉しいですよね?
1万円って、それだけ嬉しくなるくらい価値がある金額のはずです。
それなのに、高額な買い物をするとその1万円の違いが結構どうでも良くなってしまうのです。
言ってしまえば、金銭感覚が麻痺してしまうのです。
同じ「1万円」と言う価値であることは変わりないのに。
先程あげたオプションですが、車を1年乗った後に購入するかどうか、で考えてみるとどうでしょうか?
- 5万円で今あるカーナビを売って、より高性能なカーナビに変える
- 5万円で色を変える
- 10万円払ってホイール(タイヤ)をかっこよくする
- 5万円払って、明るいライトに変える。
うーん、別に買わなくていいかな・・・と思う方が多いのではないでしょうか?
もちろん、日頃からカー用品店によく行き、カスタムするのが好きな方であれば自分が思うような車を作っていくのも良いと思いますが、そこまで興味がない人が多いと思います。
それなのに新車を買うときにはオプションをどんどん乗っけてしまうのは、金銭感覚が一時的に麻痺しているからです。
普段の買い物で5円や10円の違いはあまり気にしていない方も多いでしょう。
500円の商品が遠くのスーパーが5円安い、と聞いても近くのスーパーで買物をする、私もそんなことはよくあります。
実際、5円よりも遠くのスーパーに行く時間のほうがもったいないです。笑
でも、それが例えば車になると、500万円の商品を買うときの5万円が結構どうでも良くなってしまうのです。
もともとの商品価格から1%違いがある、という点ではどちらも同じです。
そして、それがついつい金銭感覚が麻痺してしまう原因でもあります。
そのオプションに本当に数万円の価値がありますか?
車を買った1年後だとしても、それを買いますか?
そのお金があれば色々好きなことができますが、それよりも本当に欲しいものですか?
高い買い物をするときにはそのような問いかけを自分に対してすることで、絶対的な金額を考えることができるようになります。
POINT2 :大きな金額を扱うときは「絶対的な金額(割合ではなく)」を意識しよう
投資の利回り計算の「考え方」
私がいろいろな人に教えている「投資」と言うジャンルではたくさんの数字を扱うことになります。
実際に細かい計算をしていこうとするととっても難しい分野ではあるのですが、「守りの投資術」において必要な最低限の考え方をお伝えします。
必要最低限、といっても投資を考える上では非常に重要な概念です。
投資の世界ではパーセンテージ(%)をよく目にすることになります。
1000円の3%は、30円。
1000円の商品を買ったときの消費税は10%だから100円。
という、パーセンテージです。
「金利3%」を聞いて、あなたはどう考えますか?
- めっちゃお金増えそう!
- あんまり増えないよね
きっと「あんまり増えない」と思う方が多いのではないでしょうか。
1000万円持っていたとして、3%の金利を受け取ったら30万円。
1年後のお金は1030万円と、増えたのは、30万円。2年目は1030万円に対して、3%の金利がつくので受け取れる利息は30万9000円。
合計金額は1060万9000円。
やっぱりそこまで増えてないじゃないか、、1年で30万円なら、20年経っても600万円くらいでしょ?と思ってしまうのも無理はありません。
ここで考えるべきなのが「複利効果」です。
そのまま年利3%で20年間運用したらどうなるのかをグラフにしました。
| 年数 | 元利合計 | 利息 |
| 1年目 | 10,300,000 | 300,000 |
| 2年目 | 10,609,000 | 609,000 |
| 3年目 | 10,927,270 | 927,270 |
| 4年目 | 11,255,088 | 1,255,088 |
| 5年目 | 11,592,741 | 1,592,741 |
| 6年目 | 11,940,523 | 1,940,523 |
| 7年目 | 12,298,739 | 2,298,739 |
| 8年目 | 12,667,701 | 2,667,701 |
| 9年目 | 13,047,732 | 3,047,732 |
| 10年目 | 13,439,164 | 3,439,164 |
| 11年目 | 13,842,339 | 3,842,339 |
| 12年目 | 14,257,609 | 4,257,609 |
| 13年目 | 14,685,337 | 4,685,337 |
| 14年目 | 15,125,897 | 5,125,897 |
| 15年目 | 15,579,674 | 5,579,674 |
| 16年目 | 16,047,064 | 6,047,064 |
| 17年目 | 16,528,476 | 6,528,476 |
| 18年目 | 17,024,331 | 7,024,331 |
| 19年目 | 17,535,061 | 7,535,061 |
| 20年目 | 18,061,112 | 8,061,112 |
思ったよりも増えているのではないでしょうか?
20年間で受け取った利息は806万円を超えています。
たった3%でも、20年間の複利になると大きな金額になるのです。
これが、5%ではどうでしょうか?
世界経済に分散投資を行うとだいたい5%前後になると言われており、私が投資として実際に出ている利回りです。
| 年数 | 元利合計 | 利息 |
| 1年目 | 10,500,000 | 500,000 |
| 2年目 | 11,025,000 | 1,025,000 |
| 3年目 | 11,576,250 | 1,576,250 |
| 4年目 | 12,155,063 | 2,155,063 |
| 5年目 | 12,762,816 | 2,762,816 |
| 6年目 | 13,400,956 | 3,400,956 |
| 7年目 | 14,071,004 | 4,071,004 |
| 8年目 | 14,774,554 | 4,774,554 |
| 9年目 | 15,513,282 | 5,513,282 |
| 10年目 | 16,288,946 | 6,288,946 |
| 11年目 | 17,103,394 | 7,103,394 |
| 12年目 | 17,958,563 | 7,958,563 |
| 13年目 | 18,856,491 | 8,856,491 |
| 14年目 | 19,799,316 | 9,799,316 |
| 15年目 | 20,789,282 | 10,789,282 |
| 16年目 | 21,828,746 | 11,828,746 |
| 17年目 | 22,920,183 | 12,920,183 |
| 18年目 | 24,066,192 | 14,066,192 |
| 19年目 | 25,269,502 | 15,269,502 |
| 20年目 | 26,532,977 | 16,532,977 |
20年後には利息が1653万円付き、なんと元々の1000万円が2.6倍にもなりました。
これが「5%」です。
ちなみに、G-SHORKなどで有名なカシオ計算機のウェブサイトでかんたんに計算することができます。
5%と聞くと「そんなに多くないなぁ」と思うかもしれないのですが、それがここまで大きな金額になる。
これが複利効果です。
ちなみに、逆に言えば住宅ローンなどで1%の利息でお金を借りた場合に「1%なんでほぼゼロだよね」と思っていても意外と大きな金額の利息がついているということです。
積立の場合の複利効果についてはこちらの記事で詳しく開設していますが、こちらも思いのほか大きくなることがおわかりいただけるでしょう。
POINT3: 「複利効果」の大きさを知り、計算サイトを使えるようになろう!
グラフ同士のつながりがよくわからない?
ここからは「グラフ」という今までよりも「数学」っぽい話をしていきます。
難しい言葉で言えば「微分・積分」という概念なのですが、別にそんな言葉を覚えて貰う必要もなければ、当然計算ができるようになる必要も一切ありません。
大事なのは「考え方」だからです。
上で紹介した内容に比べるとちょっと高度なので、「もう覚えることが多くていっぱいいっぱい!」という方は今まで紹介したことを意識することに集中していただくのも良いかもしれません。
またいつか、この記事に戻ってきたときに読んでもらえればと思います。
新型コロナウイルスが流行して、テレビの報道などでたくさんのグラフを見る機会が増えました。
2020年6月6日時点での日本におけるコロナウイルスの感染者数を調べると、このようなグラフがありました。
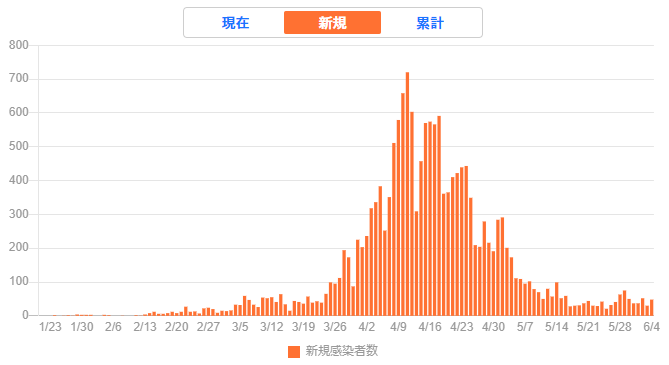

(グラフ出典:新型コロナウイルス感染症まとめ - Yahoo! JAPAN)
実はこの2つのグラフ、誤解を恐れずに言ってしまえば、全く同じデータを表しているのです。
「新規感染者数」グラフから「累計感染者数」のグラフを作ることができますし、その逆もできます。
つまり、どちらか1つのグラフがあれば、もう1つのグラフを作ることができるのです。
実はその作る方法が「微分」であり「積分」であるのですが、そんな言葉は知らなくても全く問題ありません。
上の新規感染者数グラフを見ていると、2~3月はあまり増えてなかったけど、4月はものすごい勢いで増えている。そして、5月には減っている。ということがわかると思います。
この新規感染者、つまり「増えている量」というのが、下のグラフにおける「傾き」なのです。
2~3月は傾きが緩やかで、4月は傾きが急になり、5月にはまた傾きが緩やかになっていく。
上のグラフの「大きさ」と、下のグラフの「傾き」が同じことを表しているということです。
グラフを出すときに、このようにグラフ同士の関連性や、目の前にあるグラフが何を能わしているのかがよくわかっていないと、誤解をしてしまう原因になりえます。
例えば、上の「新規感染者数」のグラフが急激に上がってきたら「感染者が増えている、ちょっとまずいな」と考えるものですが、
下の「累計感染者数」のグラフがかなり上がっているからといって「これはまずい!」のかというと、傾きが緩やかなので新規の感染者は多くないからそこまでまずくはないということになるのです。
人間は情報の大半を視覚に頼っており、グラフはその視覚情報に訴えるためとてもわかりやすいという利点があります。
しかし、それを利用することで「間違えてはないんだけど、ミスリード(誤解)させる」ことが頻繁に行われています。
保険会社のシミュレーションや、テレビに出てくるグラフなど、パット見で判断すると誤解してしまうようなグラフが溢れており、そういうことで本当は望ましくない判断をしてしまう人がたくさん出ています。
これは、非常にもったいないことです。
そんなグラフを活用(悪用)してミスリードを招く手口についてはまた別の記事で紹介したいのですが、今回はコロナウイルス関連のニュースでよく見るグラフから微分積分の「考え方」、つまり増加量を表すグラフが大きい=累計を表すグラフの傾きが大きい、ということをお話しました。
POINT: 「新規」のグラフか「累計」のグラフかを理解して、読み取れるように意識してみよう
数学的な考え方を日々の生活に役立てよう
いかがだったでしょうか。
数学の難しい計算ではなく、考え方を意識するだけで知らず識らずのうちに損をしていたり、誤解をしてしまっていたことを正しく判断することができるようになるのではないでしょうか。
合理的に考えすぎる罠についてこちらの記事で解説しました(リンク)が、人生何が何でも効率や合理性を考えればよいわけではありません。
だからといって重要ではないことに無駄にお金を使っているのはそれはそれでもったいない状態です。
豊かなモノであふれる現代、企業はあなたの時間やお金をどうやって向けてもらうかを考えてマーケティングを本気で行っています。
え、どういうこと?と思った方は以下の記事に詳しく解説してありますのでこちらも読んでみてください。
数学的な考え方を知らなければ、ミスリードや誤解に基づいてあなたの大事な時間やお金(と気力)がどんどん「あなたが本当はそこまで大事だと思っていないこと」に使われていってしまいます。
それはとてももったいないことですよね。